Localization and subdiffusive transport in quantum spin chains with dilute disorder

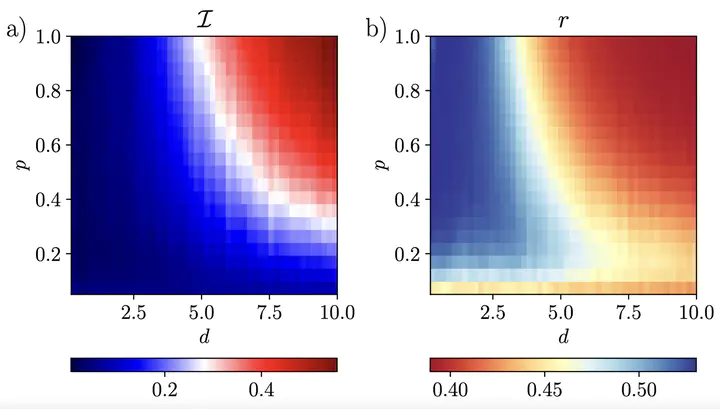
Abstract

It is widely believed that many-body localization in one dimension is fragile and can be easily destroyed by thermal inclusions; however, there are still many open questions regarding the stability of the localized phase and under what conditions it breaks down. Here I construct models with dilute disorder, which interpolate between translationally invariant and fully random models, in order to study the breakdown of localization. This opens up the possibility to controllably increase the density of thermal regions and examine the breakdown of localization as this density is increased. At strong disorder, the numerical results are consistent with commonly used diagnostics for localization even when the concentration of thermalizing regions is high. At moderate disorder, I present evidence for slow dynamics and subdiffusive transport across a large region of the phase diagram, suggestive of a “bad metal” phase. This suggests that dilute disorder may be a useful effective model for studying Griffiths effects in many-body localization, and perhaps also in a wider class of disordered systems.