Quasi-many-body localization of interacting fermions with long-range couplings
Abstract
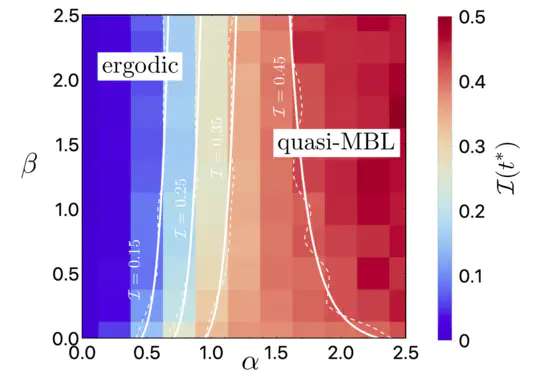
A number of experimental platforms for quantum simulations of disordered quantum matter, from dipolar systems to trapped ions, involve degrees of freedom which are coupled by power-law decaying hoppings or interactions, yet the interplay of disorder and interactions in these systems is far less understood than in their short-ranged counterpart. Here, we consider a prototype model of interacting fermions with disordered long-ranged hoppings and interactions and use the flow equation approach to map out its dynamical phase diagram as a function of hopping and interaction exponents. We demonstrate that the flow equation technique is ideally suited to problems involving long-range couplings due to its ability to accurately simulate very large system sizes. We show that at large on-site disorder and for short-range interactions, a transition from a delocalized phase to a quasi-many-body localized (MBL) phase exists as the hopping range is decreased. This quasi-MBL phase is characterized by intriguing properties such as a set of emergent conserved quantities which decay algebraically with distance. Surprisingly, we find that a crossover between delocalized and quasi-MBL phases survives even in the presence of long-range interactions.